
AlteryxでLinear Regression(線形回帰)を使った例をご紹介します。
はじめに
こんにちはSFです。今回はAlteryxでLinear Regression(線形回帰)を使った例をご紹介します。
MLB大谷翔平選手の2022年度データを使い、奪三振数が球速および球種の数の2要素とどのような関連性があるか見てみたいと思います。
サンプル概要
作成してみたワークフローがこちらとなります。
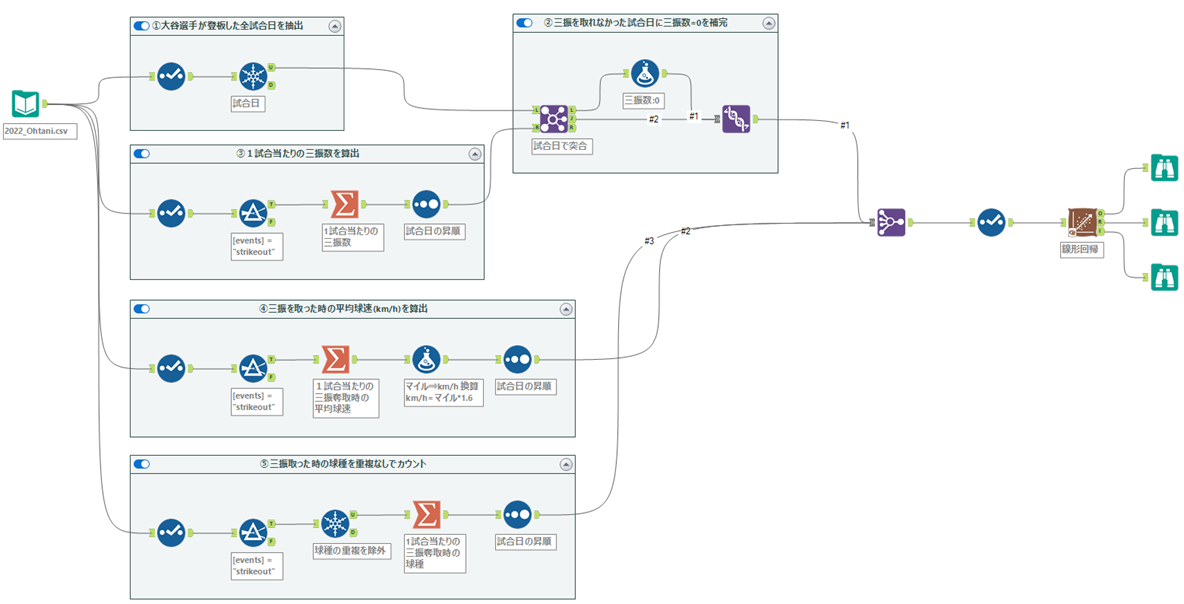
Input(データ入力)
今回のサンプルで出てくる要素(カラム)の意味は以下になります。
| カラム名 | 意味 |
| game_date | 試合日 |
| pitch_type | 球種(ストレート、カーブなど) |
| release_speed | 球速(Km/h) |
| events | 投球イベントの結果(strike_out=三振) |
※データ出典 Baseball Savant(MLB公式です)
Linear Regression (線形回帰)ツール
まずここで線形回帰分析について簡単に説明したいと思います。
予測したい情報を「ターゲット変数」、予測したい情報の値が減ったり増えたりする原因を「予測変数」などと呼びます。
取り上げた例に当てはめますと
- ターゲット変数:奪三振数
- 予測変数:球速と球種の数
の2変数となります。
線形回帰の種類として予測変数が1で単回帰モデル、2以上で重回帰モデルと呼びます。
今回は予測変数が2のため、重回帰モデルとなります。重回帰モデル式は下記となります。
奪三振数 = (係数1 × 球速) + (係数2 × 球種の数) + 切片
※係数は目的変数と説明変数の直線的な傾きを表します
サンプルWFのツールコンテナ①~⑤で求めた奪三振数(StrikeOut_Count)に対して球速(Avg_release_speed)および球種(PitchType_Count)を使って実行してみます。
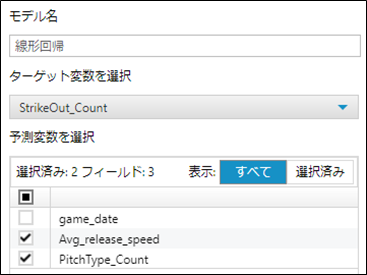
実行後の結果を確認してみます。
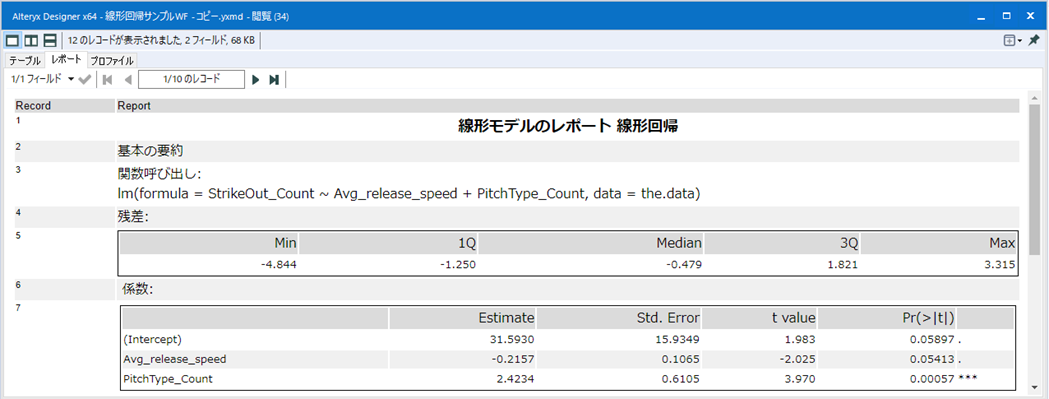
Estimateにおける値が直線回帰した関数の傾きを表しており、Interceptが切片を表しています。
球速が1上がれば奪三振数が約0.2下がり、球種の数が1上がれば奪三振数が約2.4上がると示しています。
右端の*が3つ表示されている事から重要度が高い事を示しています。(なかなか球種を増やすのも難しいと思いますが…)
まとめ
- 予測したいデータと要素の関連度合いについて、線形回帰ツールで確認する方法をご紹介しました。
 運営会社
運営会社













